Polynomial Roots
The roots of a polynomial, as you might have learned in highschool, are the intersections of the polynomial curve through the x-axis. The problem with the graphical method of finding roots is that not all of them are real. Actually, creating random polynomials will create mostly complex roots.
That is exactly what I did today. Create random polynomials, and try to find a pattern in their roots. Turns out that by plotting their roots in a complex plane a pattern emerges.
For this task I’ll use python’s scipy library, which handles polynomials quite well. More specifically, the poly1d class.
%matplotlib inline
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
A polynomial is represented by it’s coefficients, the number that multiplies every order of the variable. The class poly1d takes as argument a list with these coefficients, and, to find the roots of a polynomial we’ll use scipy’s roots function.
p = sp.poly1d([1,-2,1])
sp.roots(p)
array([ 1., 1.])
What I’ve done is plot a hundred polynomials, with coefficients 1, 0 or -1, for every order in the range 3 to 20, this means that there will be a hundred polynomials of second order, a hundred of third order, and so on… The next plot shows their position in the complex plane:
plt.figure(figsize=(16,10))
l = []
for i in range(3,21): # Degree of polynomial
for n in range(100): # How many polynomials?
p = sp.poly1d(np.random.randint(-1,2,i))
r = sp.roots(p)
for root in r:
l.append(root)
plt.scatter(r.real, r.imag, c='#00BFAD')
plt.show()
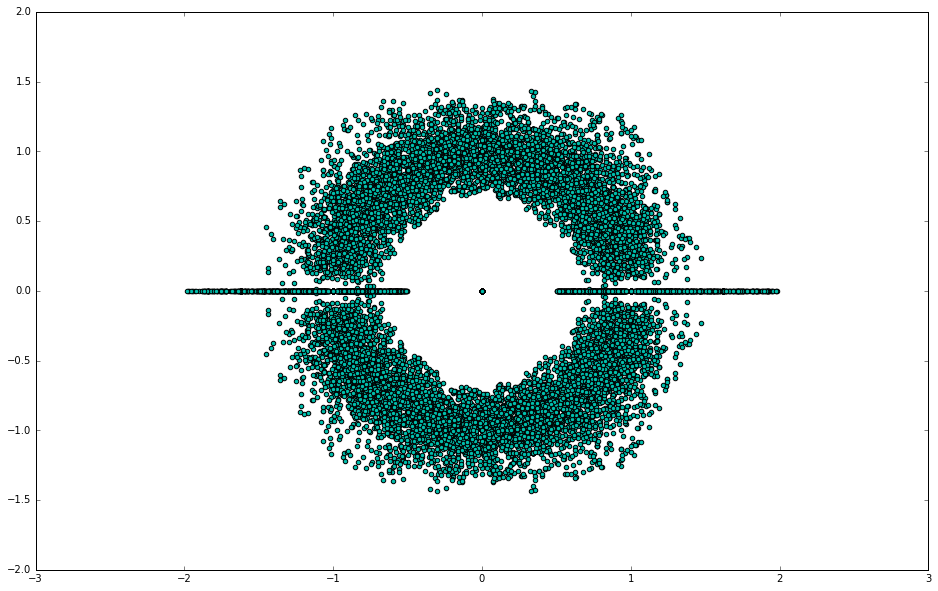
Inspecting the plot we see that all the complex roots are inscribed inside a circle of radius 1.6, but never closer than 0.5 to the center of the circle (the complex point [0,0]). The radius of these circles is only dependent of the values of the polynomial’s coefficients, and not on the order of this.
lc = []
for root in l:
if root.imag == 0:
continue
lc.append(root)
print("Maximum radius:",np.max(np.abs(lc)))
print("Minimum radius:",np.min(np.abs(lc)))
Maximum radius: 1.56747624526
Minimum radius: 0.638872422296
Real roots on the other side are much more boring, and do grow in magnitude depending on the order of the polynomial. Feel free to experiment with these on your notebooks.